Topological sorting ¶

Topological sorting¶

This example demonstrates how to get a topological sorting on a directed acyclic graph (DAG). A topological sorting of a directed graph is a linear ordering based on the precedence implied by the directed edges. It exists iff the graph doesn’t have any cycle. In igraph, we can use topological_sorting() to get a topological ordering of the vertices.

import igraph as ig

# generate a directed acyclic graph (DAG)
g = ig.Graph(
    edges=[(0, 1), (0, 2), (1, 3), (2, 4), (4, 3), (3, 5), (4, 5)],
    directed=True,
)
assert g.is_dag

# g.topological_sorting() returns a list of node IDs
# If the given graph is not DAG, the error will occur.
results = g.topological_sorting(mode='out')
print('Topological sort of g (out):', *results)

results = g.topological_sorting(mode='in')
print('Topological sort of g (in):', *results)

There are two modes of topological_sorting(). 'out' is the default mode which starts from a node with indegree equal to 0. Vice versa, the mode 'in' starts from a node with outdegree equal to 0.

The output of the code above is:

Topological sort of g (out): 0 1 2 4 3 5
Topological sort of g (in): 5 3 1 4 2 0

We can use indegree() to find the indegree of the node.

import igraph as ig

# generate directed acyclic graph (DAG)
g = ig.Graph(edges=[(0, 1), (0, 2), (1, 3), (2, 4), (4, 3), (3, 5), (4, 5)],
            directed=True)

# g.vs[i].indegree() returns the indegree of the node.
for i in range(g.vcount()):
    print('degree of {}: {}'.format(i, g.vs[i].indegree()))

'''
degree of 0: 0
degree of 1: 1
degree of 2: 2
degree of 3: 3
degree of 4: 4
degree of 5: 5
'''

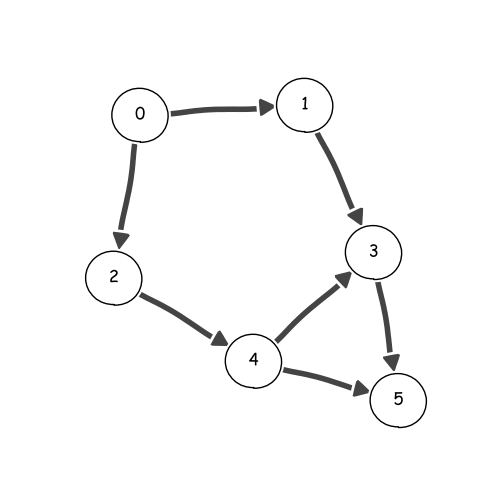
Topological sort of a directed acyclic graph (DAG) — The graph g with topological sorting.¶

We can easily plot our topologically sorted graph as follows:

import igraph as ig
import matplotlib.pyplot as plt


# generate a directed acyclic graph (DAG)
g = ig.Graph(
    edges=[(0, 1), (0, 2), (1, 3), (2, 4), (4, 3), (3, 5), (4, 5)],
    directed=True,
)

# visualization (use xkcd style for a different flavor)
with plt.xkcd():
    fig, ax = plt.subplots(figsize=(5, 5))
    ig.plot(
            g,
            target=ax,
            layout='kk',
            vertex_size=0.3,
            edge_width=4,
            vertex_label=range(g.vcount()),
            vertex_color="white",
        )

python-igraph Manual

Topological sorting ¶

Topological sorting¶