python-igraph Manual

For using igraph from Python

Erdős-Rényi Graph ¶

Erdős-Rényi Graph¶

This example demonstrates how to generate Erdős-Rényi Graphs using Erdos_Renyi(). There are two variants of graphs:

Erdos_Renyi(n, p) will generate a graph where each edge between any two pair of nodes has an independent probability p of existing.
Erdos_Renyi(n, m) will pick a graph uniformly at random out of all graphs with n nodes and m edges.

We generate two graphs of each, so we can confirm that our graph generator is truly random.

import igraph as ig
import matplotlib.pyplot as plt
import random

# Set a random seed for reproducibility
random.seed(0)

# Generate two Erdos Renyi graphs based on probability
g1 = ig.Graph.Erdos_Renyi(n=15, p=0.2, directed=False, loops=False)
g2 = ig.Graph.Erdos_Renyi(n=15, p=0.2, directed=False, loops=False)

# Generate two Erdos Renyi graphs based on number of edges
g3 = ig.Graph.Erdos_Renyi(n=20, m=35, directed=False, loops=False)
g4 = ig.Graph.Erdos_Renyi(n=20, m=35, directed=False, loops=False)

# Print out summaries of each graph
ig.summary(g1)
ig.summary(g2)
ig.summary(g3)
ig.summary(g4)

fig, axs = plt.subplots(2, 2)
# Probability
ig.plot(
    g1,
    target=axs[0, 0],
    layout="circle",
    vertex_color="lightblue"
)
ig.plot(
    g2,
    target=axs[0, 1],
    layout="circle",
    vertex_color="lightblue"
)
axs[0, 0].set_ylabel('Probability')
# N edges
ig.plot(
    g3,
    target=axs[1, 0],
    layout="circle",
    vertex_color="lightblue",
    vertex_size=0.15
)
ig.plot(
    g4,
    target=axs[1, 1],
    layout="circle",
    vertex_color="lightblue",
    vertex_size=0.15
)
axs[1, 0].set_ylabel('N. edges')
plt.show()

The received output is:

IGRAPH U--- 15 18 --
IGRAPH U--- 15 21 --
IGRAPH U--- 20 35 --
IGRAPH U--- 20 35 --

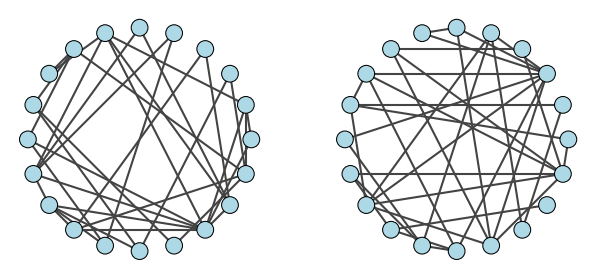
The visual representation of a randomly generated Erdős-Rényi graph — Erdős-Rényi random graphs With probability p = 0.2 (top) and with number of edges m = 35 (bottom).¶

Note

Even when using the same random seed, results can still differ depending on the machine the code is being run from.